Determining the margins of a system requires taking a statistically large-enough data collection sample size to achieve a meaningful result. The sample size takes into account variances due to silicon process, temperature, voltage, finite test time, and a number of other factors. What is the math behind this?
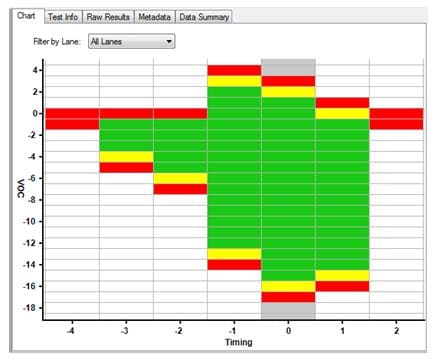
System Marginality Validation (SMV) uses on-chip embedded instrumentation to perform the margining function. Examples include Intel® Interconnect Built-In Self Test (IBIST) or Freescale™ DDR Validation Tool. The silicon embedded instruments are used in conjunction with PC-based software, such as ASSET ScanWorks®, to perform pattern generation, capture, loopback, voltage and time margining, and error checking functions, among many others. A margin run on, for example, a SATA 3 bus might look like this:
Green indicates that the no errors were encountered on the lane during the dwell time at the margining point (typically one second or thereabouts). A yellow indicates a correctable error was detected. Red indicates an undetectable error was detected.
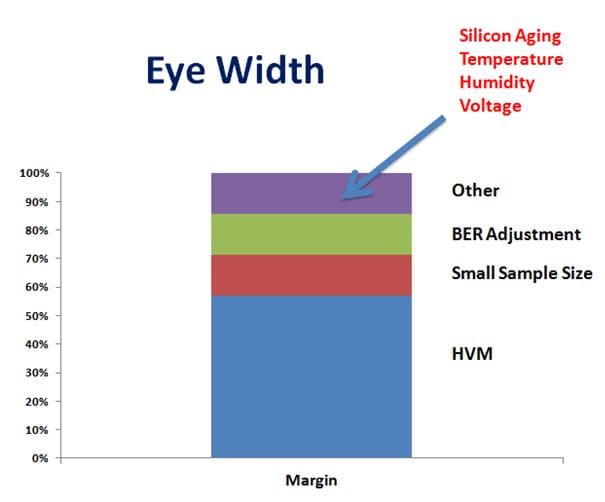
The results vary from margin run to margin run, affected by:
- Silicon high volume manufacturing (HVM) variances between and within lots
- A finite number of test samples taken
- An adjustment for the bit error rate measurable via the limited dwell time
- Chip and board effects such as temperature, voltage, humidity, silicon aging, etc.
This can be depicted visually:
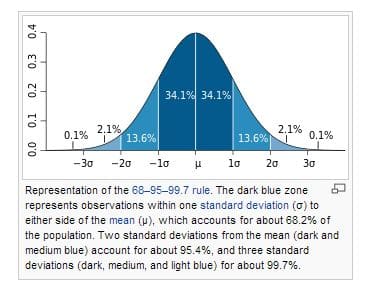
The silicon vendor takes numerous measurements across a large number of samples, constructs a normal distribution, and develops an “eye mask” perhaps based upon a 95% two-sigma (2s) or higher confidence level. The standard deviation is, according to measures of dispersion, the square root of the variance of the data set. For measurements of grouped data, the arithmetic mean and standard deviation are taken to define (1) an average that the mean of the data set must exceed, and (2) the number of measurements needed to get to the 2s confidence level.
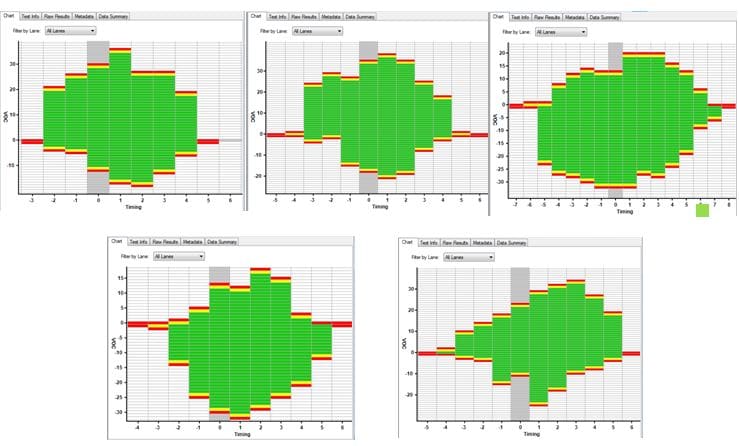
In regards to the size of the data set, both the number of measurements on one circuit board, and the number of different circuit boards tested, must be taken into account. It is known that HVM contributes a significant amount to the acceptable variance, as per our white paper: Platform Validation Using Intel® Interconnect Built-in Self Test | IBIST. Often, a 5×5 methodology is used: five unique boards with different silicon, each tested five times, for a total dataset of 25 tests. This is because there are normal distributions and variances for both chips and boards. This can be shown via some empirical data, showing a SATA margin run five times on one system:
A large amount of variability is seen from margin run to margin run. But, if the dataset of 25 is collected, and the average exceeds the defined eye mask, we know we are within a 2s or higher confidence level. But, since the process is statistical, it remains that passing the eye mask only means lower risk of system crashes or hangs; it does not guarantee that the system will work perfectly all the time. Equivalently, failing the eye mask does not necessarily mean that the system is unusable.
For more information on the 5×5 validation methodology, see our white paper, Signal Integrity Validation for Intel® Xeon® Platforms (note: registration and NDA required). For more on the technology behind the measurements of central tendency and dispersion on electronic systems, see Detection and Diagnosis of Printed Circuit Board Defects and Variances (note: registration required, but no NDA).